【知识要点】栈、队列、堆、优先队列
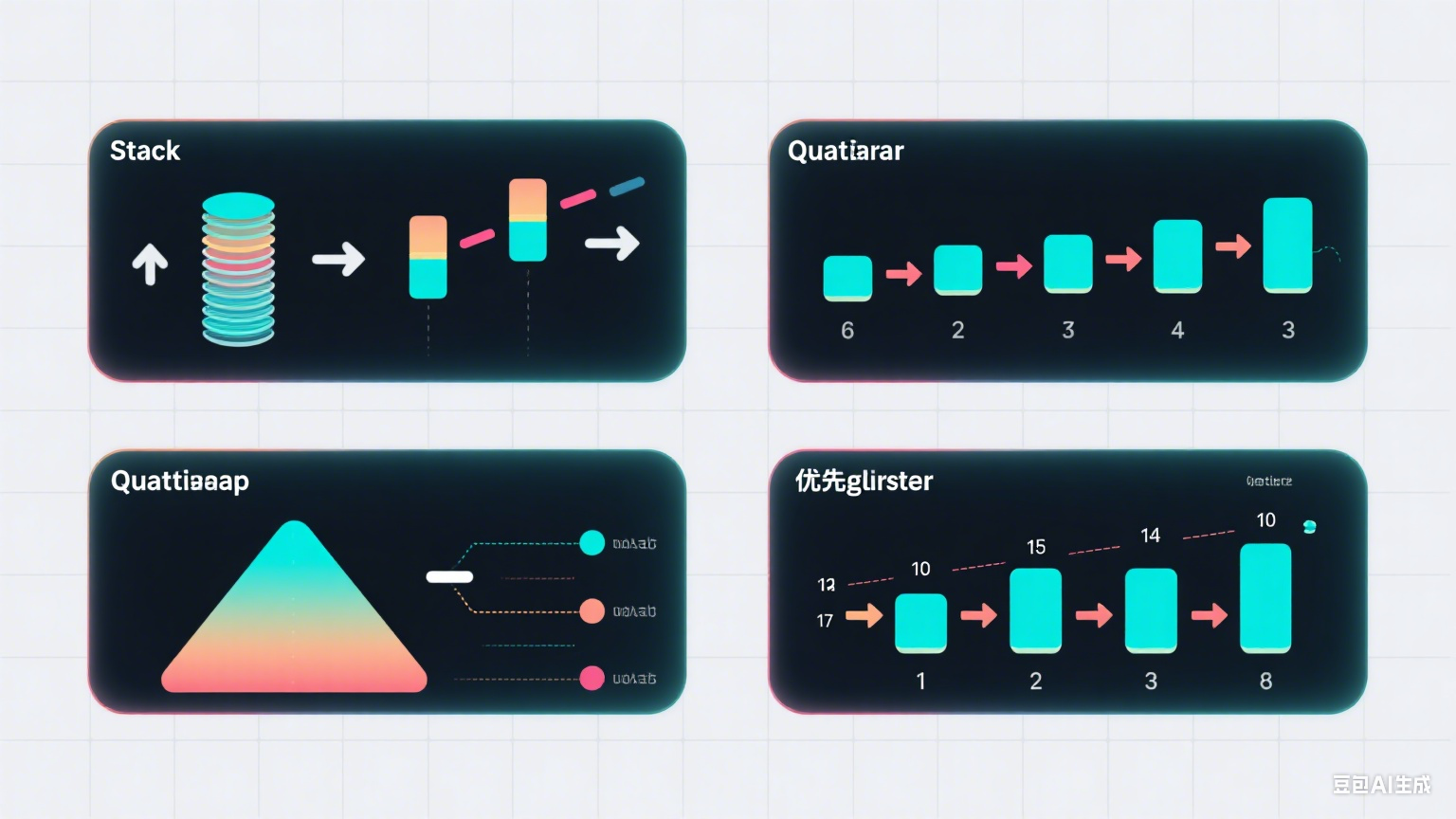
1. 栈(Stack)和队列(Queue)基础
1.1 基本概念对比
| 数据结构 | 特性 | 操作位置 | C++声明 | 插入操作 | 删除操作 |
|---|---|---|---|---|---|
| 栈(Stack) | LIFO (后进先出) | 同一端(栈顶) | stack<T> s; | s.push() | s.pop() |
| 队列(Queue) | FIFO (先进先出) | 一端插入(队尾),另一端删除(队头) | queue<T> q; | q.push() (enqueue) | q.pop() (dequeue) |
1.2 队列的详细定义
- 队列是C++标准库中的重要数据结构
- 允许删除的一端称为队头(Front)
- 允许插入的一端称为队尾(Rear)
- 空队列:队列中没有元素的状态
- 操作原则:先进先出(FIFO)
1.3 C++队列基本操作示例
#include<bits/stdc++.h>
using namespace std;
int main() {
queue<int> q; // 定义一个空队列
for(int i=0; i<5; i++) {
q.push(i); // 将i插入到队尾
}
q.emplace(32); // 将32放置到队尾,作用和push一样
cout << q.size() << endl; // 输出队列中元素的个数
while(!q.empty()) { // 当队列不为空时,继续循环
cout << q.front() << endl; // 输出队列中的首元素
q.pop(); // 将元素从队头删除
}
return 0;
}
1.4 队列queue的完整函数列表
q.pop()– 删除queue的队头元素
q.front()– 返回队列的队头元素,但不删除
q.back()– 返回队列的队尾元素,但不删除
q.push(arg)– 将元素arg插入到队列的队尾
q.emplace(arg)– 将元素arg放置到队列的尾部(效果同push)
q.size()– 返回队列中元素的个数
q.empty()– 队列为空时返回true,否则false
q.swap(q1)– 交换q和q1中的元素(交换底层数据结构)
swap(q,q1)– 非成员函数,效果同成员函数swap
1.5 队列的应用场景
- BFS(广度优先搜索)算法
- 单调队列
- 缓冲区管理
- 任务调度
2. 堆(Heap)与优先队列(Priority Queue)
2.1 堆的基本概念
- 堆是一类特殊的数据结构,常用的是二叉堆
- 形式上是一个数组,本质上是一棵完全二叉树
- 分为大根堆和小根堆:
- 大根堆:除根节点外,每个节点的值都大于等于其子节点的值
- 公式表示:A[parent(i)] >= A[i]
- 大根堆:除根节点外,每个节点的值都大于等于其子节点的值
- 小根堆:除根节点外,每个节点的值都小于等于其子节点的值
- 公式表示:A[parent(i)] <= A[i]
- 小根堆:除根节点外,每个节点的值都小于等于其子节点的值
- 分为大根堆和小根堆:
- 堆中的任一子树也还是堆
2.2 堆的基本操作
- push操作(插入):往堆尾加入元素,并通过从下往上调整保持堆性质
- get操作(删除):取出堆顶元素,用堆尾元素覆盖堆顶,再从上往下调整
2.3 优先队列的实现
C++中用priority_queue实现堆的功能:
#include <bits/stdc++.h>
using namespace std;
int main() {
// 默认大根堆
priority_queue<int> max_heap;
// 小根堆定义方式
priority_queue<int, vector<int>, greater<int>> min_heap;
// 自定义结构体的优先队列
struct Node {
int u, len;
bool operator < (const Node &x) const {
return x.len < len; // 注意这里是反向定义,实现小根堆效果
}
};
priority_queue<Node> custom_heap;
return 0;
}
2.4 优先队列的操作函数
push(Elem e)– 插入元素,时间复杂度O(log n)
pop()– 删除顶部元素,O(log n)
top()– 返回顶部元素,O(1)
size()– 返回元素数量
empty()– 判断是否为空
2.5 优先队列的特殊注意事项
- 不支持除顶部外其他元素的访问和操作
- 没有内置的clear()操作,需要手动实现:
void clear(priority_queue<int> &q) {
while (!q.empty()) q.pop();
}
- 访问top()前必须检查队列是否为空
3. 经典问题与解决方案
3.1 合并果子问题
问题描述:有n堆果子,每次合并两堆消耗体力值为两堆果子数之和,求最小总消耗。
解决方案:
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, ans = 0;
cin >> n;
priority_queue<int, vector<int>, greater<int>> q;
for(int i = 0; i < n; i++) {
int x; cin >> x;
q.push(x);
}
while(q.size() > 1) {
int x = q.top(); q.pop();
int y = q.top(); q.pop();
ans += x + y;
q.push(x + y);
}
cout << ans;
return 0;
}
时间复杂度分析:O(n log n)
3.2 互数问题
问题描述:给定素数集合S,生成由S中素数乘积构成的”互数集合”,求第n小的互数。
解决方案:
typedef long long ll;
int main() {
ll k, n;
cin >> k >> n;
vector<ll> primes(k);
priority_queue<ll, vector<ll>, greater<ll>> heap;
set<ll> seen;
for(int i = 0; i < k; i++) {
cin >> primes[i];
heap.push(primes[i]);
seen.insert(primes[i]);
}
ll humble = 1;
for(int i = 0; i < n; i++) {
humble = heap.top(); heap.pop();
for(auto p : primes) {
ll num = humble * p;
if(seen.find(num) == seen.end()) {
seen.insert(num);
heap.push(num);
}
}
}
cout << humble;
return 0;
}
时间复杂度分析:O(nk log n)
3.3 两个序列的最小N个和
问题描述:有两个长度为N的有序序列A和B,求A和B中各取一个数相加得到的N²个和中最小的N个。
解决方案:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
struct HeapNode {
int x, val;
bool operator < (const HeapNode &other) const {
return val > other.val; // 小根堆
}
};
int main() {
int n, a[maxn], b[maxn], pos[maxn] = {0};
priority_queue<HeapNode> q;
cin >> n;
for(int i = 0; i < n; i++) cin >> a[i];
for(int i = 0; i < n; i++) cin >> b[i];
// 初始时每个a[i]配b[0]
for(int i = 0; i < n; i++) {
q.push({i, a[i] + b[0]});
}
for(int i = 0; i < n; i++) {
HeapNode tmp = q.top(); q.pop();
cout << tmp.val << " ";
int x = tmp.x;
if(++pos[x] < n) {
q.push({x, a[x] + b[pos[x]]});
}
}
return 0;
}
时间复杂度分析:O(n log n)
4. 高级应用提示
- Dijkstra算法优化:堆/优先队列可用于优化Dijkstra最短路径算法,将时间复杂度从O(V²)降低到O(E + V log V)
- 单调队列:一种特殊的队列,可以高效解决滑动窗口最值问题
- 多路归并:优先队列可以高效解决多路归并问题,如上面的最小N个和问题
- Huffman编码:优先队列可用于构建最优前缀编码树
5. 总结
| 数据结构 | 特点 | 主要操作 | 时间复杂度 | 典型应用 |
|---|---|---|---|---|
| 栈(Stack) | LIFO | push, pop, top | O(1) | 函数调用、表达式求值 |
| 队列(Queue) | FIFO | push, pop, front | O(1) | BFS、缓冲区 |
| 优先队列(Priority Queue) | 自动排序 | push, pop, top | push/pop: O(log n), top: O(1) | Dijkstra、Huffman编码、合并果子 |
掌握这些基础数据结构及其应用场景,对于算法学习和编程竞赛至关重要。优先队列作为堆的高级抽象,在实际应用中更为方便,但理解其底层堆的原理同样重要。
【熟能生巧】
P9588 「MXOI Round 2」队列
题目描述
小 C 有一个队列,他要对这个队列进行 qq 次操作。操作共四种,参数分别如下:
1 x1 x:这是第一种操作,表示从队尾依次插入 1,2,3,⋯ ,x1,2,3,⋯,x;
2 y2 y:这是第二种操作,表示弹出队头的前 yy 个元素;
3 z3 z:这是第三种操作,表示查询队列中的第 zz 个元素;
44:这是第四种操作,表示查询队列中所有元素的最大值。
你需要帮助他维护这个队列,并对于每个第三种操作和第四种操作,输出查询的答案。
输入格式
第一行两个整数 c,qc,q,其中 cc 表示测试点编号。c=0c=0 表示该测试点为样例。
接下来 qq 行,每行 1∼21∼2 个整数,表示一个操作,格式见【题目描述】。
输出格式
对于每个第三种操作和第四种操作,输出一行一个整数,表示查询的答案。
输入输出样例 #1
输入 #1
0 9
1 5
1 3
2 2
1 4
3 6
3 8
2 4
4
3 3
输出 #1
3
2
4
1
说明/提示
【样例解释 #1】
在进行第四次操作后,队列中的元素依次为 3,4,5,1,2,3,1,2,3,43,4,5,1,2,3,1,2,3,4。
在进行第七次操作后,队列中的元素依次为 2,3,1,2,3,42,3,1,2,3,4。
【数据范围】
设 ∑x∑x 表示单个测试点内 xx 之和。
对于 100%100% 的数据,1≤q≤2×1051≤q≤2×105,1≤x,y,z≤1091≤x,y,z≤109,0≤∑x≤2×10140≤∑x≤2×1014,保证在进行第二种操作前队列内元素个数不小于 yy,在进行第三种操作前队列内元素个数不小于 zz,在进行第四种操作前队列内元素个数大于 00。
| 测试点编号 | q≤q≤ | x≤x≤ | ∑x≤∑x≤ | 特殊性质 |
|---|---|---|---|---|
| 1∼31∼3 | 500500 | 500500 | 2×1052×105 | C |
| 4∼84∼8 | 50005000 | 50005000 | 2×1072×107 | 无 |
| 9∼109∼10 | 2×1052×105 | 109109 | 2×10142×1014 | AB |
| 11∼1211∼12 | 2×1052×105 | 109109 | 2×10142×1014 | B |
| 13∼1413∼14 | 2×1052×105 | 109109 | 2×1092×109 | AC |
| 15∼1615∼16 | 2×1052×105 | 109109 | 2×1092×109 | C |
| 17∼1817∼18 | 2×1052×105 | 500500 | 2×1072×107 | 无 |
| 1919 | 2×1052×105 | 109109 | 2×1092×109 | 无 |
| 2020 | 2×1052×105 | 109109 | 2×10142×1014 | 无 |
特殊性质 A:没有第二种操作。
特殊性质 B:没有第三种操作。
特殊性质 C:没有第四种操作。
P2723 [USACO3.1] 丑数 Humble Numbers
题目描述
对于一给定的素数集合 S={p1,p2,…,pk}S={p1,p2,…,pk}, 考虑一个正整数集合,该集合中任一元素的质因数全部属于 SS。这个正整数集合包括,p1p1、p1×p2p1×p2、p1×p1p1×p1、p1×p2×p3p1×p2×p3 …(还有其它)。该集合被称为 SS 集合的“丑数集合”。注意:我们认为 11不是一个丑数。
你的工作是对于输入的集合 SS 去寻找“丑数集合”中的第 nn 个“丑数”。保证答案可以用 32 位有符号整数表示。
补充:丑数集合中每个数从小到大排列,每个丑数都是素数集合中的数的乘积,第 nn 个“丑数”就是在能由素数集合中的数相乘得来的(包括它本身)第 nn 小的数。
输入格式
输入的第一行是两个的整数,分别代表集合 SS 的大小 kk 和给定的参数 nn。
输入的第二行有 kk 互不相同的整数,第 ii 个整数代表 pipi。
输出格式
输出一行一个整数,代表答案。
输入输出样例 #1
输入 #1
4 19
2 3 5 7
输出 #1
27
说明/提示
数据规模与约定
对于 100%100% 的数据,保证:
- 1≤k≤1001≤k≤100。
- 1≤n≤1051≤n≤105。
- 2≤pi<2312≤pi<231,且 pipi 一定为质数。
说明
题目翻译来自 NOCOW。
USACO Training Section 3.1
P1323 删数问题
题目描述
一个集合有如下元素:11 是集合元素;若 PP 是集合的元素,则 2×P+12×P+1,4×P+54×P+5 也是集合的元素。
取出此集合中最小的 kk 个元素,按从小到大的顺序组合成一个多位数,现要求从中删除 mm 个数位上的数字,使得剩下的数字最大,编程输出删除前和删除后的多位数字。
注:不存在所有数被删除的情况。
输入格式
只有一行两个整数,分别代表 kk 和 mm。
输出格式
输出为两行两个整数,第一行为删除前的数字,第二行为删除后的数字。
输入输出样例 #1
输入 #1
5 4
输出 #1
137915
95
说明/提示
数据规模与约定
- 对于 30%30% 的数据,保证 1≤k,m≤3001≤k,m≤300。
- 对于 100%100% 的数据,保证 1≤k,m≤3×1041≤k,m≤3×104。
P2085 最小函数值
题目描述
有 nn 个函数,分别为 F1,F2,…,FnF1,F2,…,Fn。定义 Fi(x)=Aix2+Bix+Ci(x∈N∗)Fi(x)=Aix2+Bix+Ci(x∈N∗)。给定这些 AiAi、BiBi 和 CiCi,请求出所有函数的所有函数值中最小的 mm 个(如有重复的要输出多个)。
输入格式
第一行输入两个正整数 nn 和 mm。
以下 nn 行每行三个正整数,其中第 ii 行的三个数分别为 AiAi、BiBi 和 CiCi。
输出格式
输出将这 nn 个函数所有可以生成的函数值排序后的前 mm 个元素。这 mm 个数应该输出到一行,用空格隔开。
输入输出样例 #1
输入 #1
3 10
4 5 3
3 4 5
1 7 1
输出 #1
9 12 12 19 25 29 31 44 45 54
说明/提示
数据规模与约定
对于全部的测试点,保证 1≤n,m≤100001≤n,m≤10000,1≤Ai≤101≤Ai≤10, 0≤Bi≤1000≤Bi≤100, 0≤Ci≤1040≤Ci≤104。
【答案校对】
队列
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=800010;
int c,T,t,i,cnt,op,x,del,qwq,f[N],l[N],r[N],a[N*2],h=1,n=400005;
int read(){
int f=1,x=0;char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return f*x;
}
void update(int x,int l,int r,int ql,int qr,int k){
int mid=(l+r)>>1;
if(ql<=l&&r<=qr){
a[x]=k;return;
}
if(ql<=mid) update(x*2,l,mid,ql,qr,k);
if(qr>mid) update(x*2+1,mid+1,r,ql,qr,k);
a[x]=max(a[x*2],a[x*2+1]);
}
int query(int x,int l,int r,int ql,int qr){
int mid=(l+r)>>1,sum=0;
if(ql<=l&&r<=qr){
return a[x];
}
if(ql<=mid) sum=max(sum,query(x*2,l,mid,ql,qr));
if(qr>mid) sum=max(sum,query(x*2+1,mid+1,r,ql,qr));
return sum;
}
signed main(){
cin>>c>>T;
while(T--){
op=read();
if(op==1)
x=read(),l[++t]=1,r[t]=x,update(1,1,n,t,t,x),f[t]=f[t-1]+x;
else if(op==2){
x=read();cnt=0;
for(i=h;i<=t;++i){
cnt+=r[i]-l[i]+1;
if(cnt>=x){
cnt-=r[i]-l[i]+1;
l[i]+=x-cnt;del+=x-cnt;
if(l[i]>r[i])update(1,1,n,i,i,0),++h;
break;
}
del+=r[i]-l[i]+1;r[i]=l[i]=0;++h;
update(1,1,n,i,i,0);
}
}
else if(op==3){
x=read();
qwq=lower_bound(f+h,f+t+1,del+x)-f;
printf("%lld\n",del+x-f[qwq-1]);
}
else printf("%lld\n",query(1,1,n,h,t));
}
}
丑数
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,m,i,j,a[105],b[105],s[100005],zx;
signed main(){
cin>>n>>m;
for(i=1;i<=n;i++)
cin>>a[i];
s[0]=1;
for(i=1;i<=m;i++){
zx=pow(2,31)-1;
for(j=1;j<=n;j++){
while(a[j]*s[b[j]]<=s[i-1])
b[j]++;
if(a[j]*s[b[j]]<zx)
zx=a[j]*s[b[j]];
}
s[i]=zx;
}
cout<<s[m];
}
删数问题
#include <bits/stdc++.h>
#define int long long
using namespace std;
priority_queue<int,vector<int>,greater<int> > q;
string p;
int k,m,s;
signed main(){
ios::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
cin>>k>>m;
q.push(1);
while(k){
int s=q.top();
p=p+to_string(s);
q.pop();
q.push(s*2+1);
q.push(s*4+5);
k--;
}
cout<<p<<"\n";
while(true){
for(int i=0;i<p.size();i++){
if(p[i+1]>p[i]){
s++;
p.erase(i,1);
if(s>=m){
cout<<p;
exit(0);
}
break;
}
}
}
}
最小函数值
#include <bits/stdc++.h>
#define int long long
using namespace std;
int a[10001],b[10001],c[10001],n,m,s[10000001],i,j,t;
signed main(){
cin>>n>>m;
for(i=1;i<=n;i++) cin>>a[i]>>b[i]>>c[i];
for(i=1;i<=n;i++) for(j=1;j<=100;j++) s[++t]=a[i]*j*j+b[i]*j+c[i];
sort(s+1,s+1+t);
for(i=1;i<=m;i++) cout<<s[i]<<" ";
}








暂无评论内容